Pierre Bénard 16 Janvier 2006La réfraction atmosphérique en montagne
Cette page montre comment calculer les effets de la réfraction atmosphérique pour connaître la déformation du paysage en montagne. La méthode décrite ici utilise une discrétisation spatiale du rayon lumineux le long de sa trajectoire, mais elle retient la valeur exacte de l'indice de réfraction en chaque point de l'espace, ce qui conduit à des résultats beaucoup plus précis que des méthodes pour lesquelles le champ d'indice de réfraction est décrit par une approximation discrète fixée a priori. La différence entre la méthode utilisée ici et ces méthodes moins précises est abordée dans l'Appendice B.
Les effets de la réfraction atmosphérique (mirages, déformations, déviations...) sont dus
au fait que l'indice de réfraction de l'atmosphère (noté "![]() " dans la suite) n'est pas constant et uniforme dans l'espace,
mais présente des variations locales qui viennent dévier les rayons lumineux par rapport
à une trajectoire rectiligne. L'indice de réfraction
n'est autre que le rapport de la vitesse de la lumière dans le vide à celle observée dans le
milieu réfringent (ici, l'atmosphère). Au cours de leur voyage d'un point à un autre, les rayons lumineux
adoptent le trajet qui minimise le temps de parcours, et qui n'est donc pas nécessairement
la ligne droite si l'indice de réfraction varie dans l'espace dans la région du trajet.
" dans la suite) n'est pas constant et uniforme dans l'espace,
mais présente des variations locales qui viennent dévier les rayons lumineux par rapport
à une trajectoire rectiligne. L'indice de réfraction
n'est autre que le rapport de la vitesse de la lumière dans le vide à celle observée dans le
milieu réfringent (ici, l'atmosphère). Au cours de leur voyage d'un point à un autre, les rayons lumineux
adoptent le trajet qui minimise le temps de parcours, et qui n'est donc pas nécessairement
la ligne droite si l'indice de réfraction varie dans l'espace dans la région du trajet.
Il est important de souligner qu'il n'existe pas d'expression simple et universelle
donnant la valeur exacte de l'indice de réfraction atmosphérique en un point donné et
à un instant donné, car l'indice de réfraction dépend d'une multitude de paramètres
eux-mêmes variables dans le temps et dans l'espace (température, pression,...).
En conséquence, selon l'application que l'on veut faire des calculs de réfraction, il faut
bien analyser quelle sont les dépendances de ![]() par rapport aux différents paramètres
qui doivent être retenues et quelles sont celles que l'on peut négliger.
par rapport aux différents paramètres
qui doivent être retenues et quelles sont celles que l'on peut négliger.
Par exemple, selon que l'on voudra comprendre et calculer de mirages inversés, ou bien l'apparition du "rayon vert", ou encore, comme ici, la déformation du paysage en montagne, les paramètres à prendre en considération dans le calcul de l'indice de réfraction ne seront pas les mêmes. Pour calculer le "rayon vert", il faut évidemment tenir compte des variations de l'indice de réfraction en fonction de la longueur d'onde de la lumière, alors que cet aspect peut être négligé pour calculer la déformation du paysage en montagne, et ainsi de suite...
La formule donnant l'indice de réfraction que nous utilisons comme point de départ pour les calculs ci-dessous ne saurait donc être prise pour argent comptant en vue d'une application différente de celle qui en est faite ici. Néanmoins, en vue d'applications différentes, on pourra toujours tenter de s'inspirer des considérations conduisant à la justification de la formule utilisée ici, et qui sont exposées tout en bas de ce document, dans l'appendice A.
Avec une approximation raisonnable pour ce que nous voulons en faire ici, nous considérerons que les variations de l'indice de réfraction sont uniquement dues à la variation de la densité de l'air sec dans l'atmosphère, et nous supposerons en outre que cette densité est celle de "l'atmosphère standard", c'est à dire une atmosphère homogène horizontalement, et présentant un profil vertical proche de celui celui qui est observé en moyenne sur notre planète.
Ce faisant, nous négligeons donc les effets de réfraction liés à la présence d'autres constituants que l'air sec dans l'atmosphère, notamment la vapeur d'eau. Nous négligeons également de prendre en compte l'état thermique exact de l'atmosphère pour nous concentrer sur l'état standard (qui est un état moyen). Donc l'effet calculé peut différer légèrement d'une observation particulière si l'observation se déroule alors que l'état de l'atmosphère diffère notablement de l'état standard. En outre, comme évoqué plus haut, nous négligeons la dépendance de l'indice de réfraction par rapport à la longueur d'onde du rayonnement.
Pour calculer les effets de la réfraction atmosphérique, il faut d'abord
connaître comment varie l'indice de réfraction de l'air "![]() " en fonction du lieu,
puis il faut connaître la loi de propagation de la lumière dans l'air. Ces deux
aspects sont abordés dans cette section.
" en fonction du lieu,
puis il faut connaître la loi de propagation de la lumière dans l'air. Ces deux
aspects sont abordés dans cette section.
Pour les problèmes qui nous intéressent, comme expliqué dans l'Appendice A, l'indice de réfraction peut être estimé par la formule suivante:
où la signification physique des constantes est donnée dans l'Appendice A.
Dans cette formule, ![]() est l'altitude (en m), et les températures
est l'altitude (en m), et les températures
![]() sont des températures absolues, en Kelvin.
sont des températures absolues, en Kelvin.
Pour les applications, nous choisirons les valeurs suivantes:
- ![]() 101325. Pa (soit 1 Atm)
101325. Pa (soit 1 Atm)
- ![]() 273.16 K (soit
273.16 K (soit ![]() C)
C)
- ![]() 1.00029
1.00029
- ![]() 10000 m
10000 m
- ![]() 0.0065 K/m
0.0065 K/m
Ainsi, les valeurs de ![]() au niveau de la mer sont, avec
cette formule:
au niveau de la mer sont, avec
cette formule:
- ![]() 273.16 K (soit
273.16 K (soit ![]() C) :
C) : ![]() =1.00029
=1.00029
- ![]() 283.16 K (soit
283.16 K (soit ![]() C) :
C) : ![]() =1.00028
=1.00028
- ![]() 293.16 K (soit
293.16 K (soit ![]() C) :
C) : ![]() =1.00027
=1.00027
Ensuite, l'indice diminue rapidement avec l'altitude: pour ![]() K (soit
K (soit ![]() C),
on a:
C),
on a:
- ![]() = 0 km:
= 0 km: ![]() =1.00028
=1.00028
- ![]() = 1 km:
= 1 km: ![]() =1.00025
=1.00025
- ![]() = 2 km :
= 2 km : ![]() =1.00023
=1.00023
- ![]() = 3 km :
= 3 km : ![]() =1.00021
=1.00021
Lorsqu'on applique la forme (1) indiquée ci-dessus pour l'indice de réfraction,
on s'aperçoit (après avoir effectué tous les calculs décrits ci-après) que les
résultats dépendent en fait assez peu de la température au niveau de la mer ![]() .
On peut donc
utiliser partout
.
On peut donc
utiliser partout ![]() =283.16 K sans commettre une erreur trop importante, et
c'est ce que nous faisons désormais.
=283.16 K sans commettre une erreur trop importante, et
c'est ce que nous faisons désormais.
La loi de propagation de la lumière dans l'air s'écrit:
| (2) |
où ![]() est le vecteur unitaire tangent au
rayon de lumière et
est le vecteur unitaire tangent au
rayon de lumière et ![]() est l'abcisse
curviligne le long du rayon de lumière. Le symbole
est l'abcisse
curviligne le long du rayon de lumière. Le symbole ![]() désigne le vecteur gradient de l'indice de réfraction.
désigne le vecteur gradient de l'indice de réfraction.
Dans notre cas, ![]() ne dépend que de
ne dépend que de ![]() et donc
et donc
| (3) |
où ![]() est le vecteur unitaire dans la direction verticale ascendante.
L'expression de la dérivée verticale de l'indice de réfraction en fonction de l'altitude
est donnée par l'Appendice A:
est le vecteur unitaire dans la direction verticale ascendante.
L'expression de la dérivée verticale de l'indice de réfraction en fonction de l'altitude
est donnée par l'Appendice A:
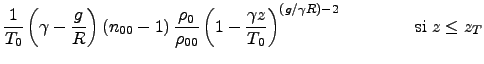 |
|||
![$\displaystyle \frac{- g}{R T_T}(n_{00} -1) \frac{\rho_T}{\rho_{00}}\; \exp \left[- \frac{g }{R T_T} (z-z_T)\right]\;\;\;\;\;\;\;\;\;\;\;\;\; {\rm si \;} z > z_T$](img27.png) |
(4) |
D'autre part, si ![]() est un point courant sur le rayon optique et
est un point courant sur le rayon optique et ![]() le vecteur joignant
le vecteur joignant ![]() à
à ![]() , on a, par construction:
, on a, par construction:
| (5) |
On se place dans le plan formé par le centre de la Terre, le point
d'observation ![]() et le point observé
et le point observé ![]() .
On définit dans ce plan un repère Cartésien direct
.
On définit dans ce plan un repère Cartésien direct ![]() ou
ou ![]() est le centre de la Terre et
est le centre de la Terre et ![]() pointe vers
pointe vers ![]() .
Les vecteurs n'ont
donc que deux composantes: selon
.
Les vecteurs n'ont
donc que deux composantes: selon ![]() et selon
et selon ![]() .
Les variables du problème sont
.
Les variables du problème sont ![]() ,
, ![]() et le vecteur position des points sur le rayon optique:
et le vecteur position des points sur le rayon optique: ![]() .
Les vecteurs étant décomposés selon
.
Les vecteurs étant décomposés selon ![]() et
et ![]() , on a:
, on a:
![]() et
et
![]() .
.
Pour chaque point, connaissant ses coordonnées ![]() , il faut être
capable de connaître son altitude
, il faut être
capable de connaître son altitude ![]() . La terre étant ici supposée sphérique de rayon
. La terre étant ici supposée sphérique de rayon
![]() , l'altitude
, l'altitude ![]() d'un point de coordonnées
d'un point de coordonnées ![]() est donnée par:
est donnée par:
| (6) |
La Figure 1 montre le positionnement de ![]() ,
, ![]() et la signification de
et la signification de ![]() .
.
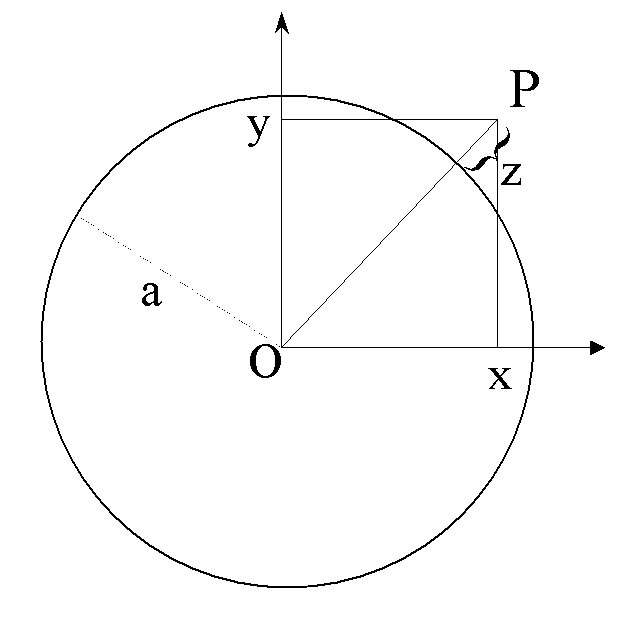
Figure 1: Coordonnées ![]() et altitude
et altitude ![]() pour un point
pour un point ![]() donné.
Le rayon terrestre est noté
donné.
Le rayon terrestre est noté ![]() .
.
Rappelons que l'angle que forme le rayon d'une visée par rapport au plan horizontal, s'appelle le "site" de cette visée (c'est un terme d'artillerie). Pour les visées dirigées vers le bas, le site est négatif.
Le but du problème est de déterminer le rayon lumineux joignant ![]() à
à ![]() . Ceci nous permettra de résoudre l'ensemble des problèmes
que l'on peut se poser:
. Ceci nous permettra de résoudre l'ensemble des problèmes
que l'on peut se poser:
Comme les variations de ![]() n'ont pas une
expression simple, on ne peut pas espérer résoudre simplement le problème par une
méthode analytique (c'est à dire à la main, avec un papier et un crayon).
Donc, on adopte une méthode numérique: on découpe le
rayon lumineux en une succession de petits trajets de longueur
n'ont pas une
expression simple, on ne peut pas espérer résoudre simplement le problème par une
méthode analytique (c'est à dire à la main, avec un papier et un crayon).
Donc, on adopte une méthode numérique: on découpe le
rayon lumineux en une succession de petits trajets de longueur ![]() et pour chacun
de ces petits trajets on applique les équations de propagation grâce à une discrétisation
de ces équation sous forme de différences finies, en appliquant les valeurs locales
des variables nécessaires au calcul. Pour résoudre l'équation il faut alors un ordinateur,
et il faut écrire le programme qui résoudra le problème.
et pour chacun
de ces petits trajets on applique les équations de propagation grâce à une discrétisation
de ces équation sous forme de différences finies, en appliquant les valeurs locales
des variables nécessaires au calcul. Pour résoudre l'équation il faut alors un ordinateur,
et il faut écrire le programme qui résoudra le problème.
Un point important est de bien veiller respecter à le principe de retour inverse de la
lumière, sous peine d'imprécision dans les résultats: on s'impose donc de trouver le même
résultat selon que l'on vise du point ![]() ou du point
ou du point ![]() , car si
, car si ![]() voit
voit ![]() , alors
, alors
![]() doit voir
doit voir ![]() par le même rayon lumineux.
par le même rayon lumineux.
Ici, on commence par s'attaquer à un problème plus simple, qui est de calculer
la trajectoire d'un rayon optique pour une visée donnée. On se fixe donc le point de visée ![]() et le site de visée
et le site de visée ![]() , et on calcule d'abord la trajectoire suivie par le rayon lumineux, de
proche en proche, comme expliqué ci-dessus.
Ensuite, puisqu'il faut bien s'arrêter de calculer au bout d'un certain temps, on spécifie
une condition d'arrêt de calcul.
, et on calcule d'abord la trajectoire suivie par le rayon lumineux, de
proche en proche, comme expliqué ci-dessus.
Ensuite, puisqu'il faut bien s'arrêter de calculer au bout d'un certain temps, on spécifie
une condition d'arrêt de calcul.
Rappelons que les équations à discrétiser sont:
| (7) | |||
| (8) |
On divise le rayon optique en petits segments de longueur ![]() , et donc on suppose
que le rayon est décrit par une suite de points
, et donc on suppose
que le rayon est décrit par une suite de points ![]() et de vecteurs unitaires tangents
et de vecteurs unitaires tangents ![]() , qu'il
nous faut calculer. L'indice de réfraction à ce point
, qu'il
nous faut calculer. L'indice de réfraction à ce point ![]() est noté
est noté ![]() . Les équations discrétisées s'écrivent alors:
. Les équations discrétisées s'écrivent alors:
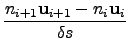 |
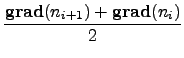 |
(9) | |
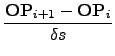 |
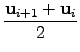 |
(10) |
On suppose connus ![]() et
et ![]() et on veut calculer le point suivant:
et on veut calculer le point suivant: ![]() ,
et le vecteur unitaire tangent au rayon au point suivant:
,
et le vecteur unitaire tangent au rayon au point suivant: ![]() , ainsi que l'indice de réfraction
au point suivant
, ainsi que l'indice de réfraction
au point suivant ![]() . Comme on s'est imposé une discrétisation "implicite" (c'est à dire symétrique)
afin d'assurer la contrainte du retour inverse de la lumière, les inconnues
apparaissent à plusieurs endroits, et il n'est pas simple de résoudre le système précédent par une
méthode directe. On utilise donc une méthode itérative. D'abord on calcule un estimateur
(noté
. Comme on s'est imposé une discrétisation "implicite" (c'est à dire symétrique)
afin d'assurer la contrainte du retour inverse de la lumière, les inconnues
apparaissent à plusieurs endroits, et il n'est pas simple de résoudre le système précédent par une
méthode directe. On utilise donc une méthode itérative. D'abord on calcule un estimateur
(noté ![]() ) du point suivant
) du point suivant ![]() et les variables associées:
et les variables associées:
Une fois connu l'estimateur ![]() et toutes les variables associés, on
applique le processus itératif en lui-même.
Pour un indice d'itération noté
et toutes les variables associés, on
applique le processus itératif en lui-même.
Pour un indice d'itération noté ![]() , on applique l'algorithme itératif suivant:
, on applique l'algorithme itératif suivant:
Du fait de la faible non-linéarité des équations, l'algorithme converge extrêmement rapidement, et en pratique une seule
itération est nécessaire pour arriver à une grande précision. Donc, connaissant un point ![]() sur le rayon lumineux,
le point suivant sur la trajectoire est donné par:
sur le rayon lumineux,
le point suivant sur la trajectoire est donné par:
| (11) |
On voit que la contrainte de respect du principe de retour inverse de la lumière n'est qu'imparfaitement respectée puisqu'on ne fait qu'une seule itération, ce qui ne garantit pas que les équations de la discrétisation symétrique sont exactement résolues. Toutefois puisque la convergence du processus itératif est très rapide, la contrainte est respectée avec une bonne précision, en tout cas suffisante pour notre problème.
On voit également que la pécision du calcul dépendra de la longueur des segments
![]() que l'on a choisi. Si on prend
que l'on a choisi. Si on prend ![]() aussi long que la distance entre
aussi long que la distance entre ![]() et
et
![]() , la précision sera très mauvaise, puisque le rayon modélisé joignant les deux points ne sera
pas une courbe mais un segment de droite. Dans tous les calculs que je décris, j'ai utilisé
la valeur
, la précision sera très mauvaise, puisque le rayon modélisé joignant les deux points ne sera
pas une courbe mais un segment de droite. Dans tous les calculs que je décris, j'ai utilisé
la valeur
![]() ou
ou ![]() , qui donne une précision largement compatible avec nos objectifs.
Bien évidemment, plus on choisit
, qui donne une précision largement compatible avec nos objectifs.
Bien évidemment, plus on choisit ![]() petit, plus la précision du calcul est bonne, mais
aussi, plus le calcul est long, car il faut décomposer le rayon lumineux joignant
petit, plus la précision du calcul est bonne, mais
aussi, plus le calcul est long, car il faut décomposer le rayon lumineux joignant ![]() et
et ![]() en un plus grand nombre de segments, qu'il faut alors calculer un par un à la suite l'un de l'autre.
en un plus grand nombre de segments, qu'il faut alors calculer un par un à la suite l'un de l'autre.
Pour pouvoir débuter le calcul, il faut spécifier le point de visée qui, par construction, a pour coordonnées:
| (12) |
où ![]() est l'altitude du point. Il faut également spécifier l'angle de visée (le site de visée)
que nous appelerons
est l'altitude du point. Il faut également spécifier l'angle de visée (le site de visée)
que nous appelerons ![]() . Les composantes du vecteur
. Les composantes du vecteur ![]() tangent au rayon au point
tangent au rayon au point ![]() sont alors:
sont alors:
| (13) | |||
| (14) |
Il faut nécessairement spécifier une fin au calcul de la trajectoire du rayon.
En pratique, ce qui nous intéresse c'est d'arrêter le calcul une fois que le rayon a franchi
la distance qui sépare le point de visée ![]() du point observé
du point observé ![]() . Seulement
comme le rayon est courbé, ce n'est pas la distance le long du rayon qu'il faut
considérer, mais la distance absolue sur la Terre. On commence donc par mesurer
la distance sur la Terre du point observé
. Seulement
comme le rayon est courbé, ce n'est pas la distance le long du rayon qu'il faut
considérer, mais la distance absolue sur la Terre. On commence donc par mesurer
la distance sur la Terre du point observé ![]() par rapport au point de visée
par rapport au point de visée ![]() .
En fait c'est la distance angulaire
.
En fait c'est la distance angulaire
![]() entre ces deux points que l'on utilise, c'est
à dire l'angle formé par les deux rayons
entre ces deux points que l'on utilise, c'est
à dire l'angle formé par les deux rayons ![]() , où
, où ![]() est, rappelons le,
le centre de la Terre. Si
est, rappelons le,
le centre de la Terre. Si ![]() est la distance sur la Terre en les deux points,
cette distance angulaire
est la distance sur la Terre en les deux points,
cette distance angulaire
![]() est donnée par:
est donnée par:
| (15) |
où ![]() et
et ![]() sont en km et
sont en km et
![]() est en Radians. Si on ne connaît
pas la distance terrestre (qui est difficile à mesurer sur une carte pour des grandes distances,
à cause des déformations liées à la projection utilisée pour obtenir une carte plate), on
peut alors faire un calcul plus compliqué à partir des coordonnées géographiques des points
est en Radians. Si on ne connaît
pas la distance terrestre (qui est difficile à mesurer sur une carte pour des grandes distances,
à cause des déformations liées à la projection utilisée pour obtenir une carte plate), on
peut alors faire un calcul plus compliqué à partir des coordonnées géographiques des points
![]() et
et ![]() . Mais jusqu'à 500 km, on peut normalement se contenter de mesurer directement
la distance avec une règle sur la carte sans trop d'erreur.
. Mais jusqu'à 500 km, on peut normalement se contenter de mesurer directement
la distance avec une règle sur la carte sans trop d'erreur.
Pendant le calcul de la trajectoire de notre rayon, nous pouvons donc calculer
pour chaque point
![]() la distance angulaire sur la Terre déjà parcourue par le rayon:
la distance angulaire sur la Terre déjà parcourue par le rayon:
| (16) |
Il suffit donc d'arrêter le calcul dès que
![]() . C'est à dire
dès que le rayon lumineux aura dépassé la verticale du point observé.
. C'est à dire
dès que le rayon lumineux aura dépassé la verticale du point observé.
Il est important de remarquer que
comme ici nous avons spécifié ![]() de manière libre ou au hasard, rien ne garantit que notre
rayon passe bien au point
de manière libre ou au hasard, rien ne garantit que notre
rayon passe bien au point ![]() lorsque la distance
lorsque la distance
![]() est franchie: il peut très bien
passer au-dessus si
est franchie: il peut très bien
passer au-dessus si ![]() a été choisi trop grand, soit au-dessous dans le cas inverse.
Dans la prochaine section on va s'intéresser à trouver la valeur de
a été choisi trop grand, soit au-dessous dans le cas inverse.
Dans la prochaine section on va s'intéresser à trouver la valeur de ![]() qui permet au rayon d'atteindre exactement le point
qui permet au rayon d'atteindre exactement le point ![]() .
.
On peut calculer l'erreur par rapport à la cible ![]() . Pour cela on enregistre
l'altitude
. Pour cela on enregistre
l'altitude ![]() du rayon au dernier point de trajectoire précédant
la cible
du rayon au dernier point de trajectoire précédant
la cible ![]() , et dont la distance angulaire avec
, et dont la distance angulaire avec ![]() est notée
est notée
![]() .
De même on enregistre l'altitude du rayon au point suivant
.
De même on enregistre l'altitude du rayon au point suivant ![]() ,
qui est le premier point de trajectoire ayant dépassé la cible, et dont la distance
angulaire avec
,
qui est le premier point de trajectoire ayant dépassé la cible, et dont la distance
angulaire avec ![]() est notée
est notée
![]() .
On calcule alors l'altitude du rayon sur ce segment au moment où il dépasse la cible
par une interpolation linéaire:
.
On calcule alors l'altitude du rayon sur ce segment au moment où il dépasse la cible
par une interpolation linéaire:
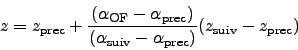 |
(17) |
Maintenant on calcule la trajectoire du rayon qui joint exactement les deux points
qui nous intéressent: ![]() et
et ![]() . Pour cela nous adoptons simplement une méthode par
"essai-erreur", en réduisant successivement l'erreur au moyen d'un nouveau processus itératif.
Rappelons que l'on note
. Pour cela nous adoptons simplement une méthode par
"essai-erreur", en réduisant successivement l'erreur au moyen d'un nouveau processus itératif.
Rappelons que l'on note ![]() l'altitude du point d'observation
l'altitude du point d'observation ![]() , et
, et ![]() l'altitude
du point cible
l'altitude
du point cible ![]() .
.
Tout d'abord, on spécifie un
![]() qui vise à coup sûr
au-dessus de la cible, et un
qui vise à coup sûr
au-dessus de la cible, et un
![]() qui vise à coup sûr
au-dessous de la cible. En pratique, on prend par exemple
qui vise à coup sûr
au-dessous de la cible. En pratique, on prend par exemple
![]() Rad,
et
Rad,
et
![]() Rad. Pour ces deux valeurs initiales, on calcule
l'altitude obtenue lorsque le rayon atteint la distance de la cible, que l'on note
Rad. Pour ces deux valeurs initiales, on calcule
l'altitude obtenue lorsque le rayon atteint la distance de la cible, que l'on note
![]() et
et ![]() . On en déduit donc les erreurs survenues pour ces
deux visées.
. On en déduit donc les erreurs survenues pour ces
deux visées.
Ensuite, on applique le processus itératif d'essais-erreurs lui-même:
On réitère ce processus un nombre fixé de fois (en pratique une dizaine d'itérations suffisent). En imprimant l'erreur d'altitude finale par rapport à la cible, on s'assure que la précision atteinte est celle que l'on désire, sinon, il faut augmenter le nombre d'itérations. L'erreur diminue très vite, d'un facteur 10 à 100 à chaque nouvelle itération. On notera que cette méthode est exactement celle qui est utilisée par les artilleurs, dont le problème se pose d'ailleurs en termes très proches (cette méthode nécessite toutefois la possibilité de pouvoir estimer visuellement l'erreur du tir d'artillerie par rapport à la cible, au moyen d'observateurs avancés, ou placés sur des hauteurs avoisinantes).
Nous sommes maintenant capables de calculer le site de visée ![]() qu'il faut adopter
à partir de notre point d'observation pour que le rayon lumineux atteigne effectivement le
point observé.
qu'il faut adopter
à partir de notre point d'observation pour que le rayon lumineux atteigne effectivement le
point observé.
Maintenant, nous savons déterminer la trajectoire d'un rayon lumineux
pour qu'il aboutisse en un point donné, et donc nous pouvons calculer le site
de visée ![]() pour observer ce point: il suffit de spécifier l'altitude
pour observer ce point: il suffit de spécifier l'altitude ![]() du point
d'observation (pour le Pic de Saint-Barthélemy, 2348m), la distance angulaire
du point observé
du point
d'observation (pour le Pic de Saint-Barthélemy, 2348m), la distance angulaire
du point observé ![]() et son altitude
et son altitude ![]() . L'algorithme que nous avons
détaillé ci-dessus donne alors le site apparent du point observé.
. L'algorithme que nous avons
détaillé ci-dessus donne alors le site apparent du point observé.
Si on veut calculer la distance de l'horizon optique
observé à partir d'une altitude donnée ![]() ,
on peut se servir du même programme en le modifiant très légèrement:
On suppose une altitude du point de visée
,
on peut se servir du même programme en le modifiant très légèrement:
On suppose une altitude du point de visée ![]() égale à zéro, et un site de visée
égale à zéro, et un site de visée
![]() égal à zéro lui aussi. On peut calculer la trajectoire du rayon de visée par
la méthode indiquée précédemment. Puisque l'observateur est au ras de la mer
et vise à l'horizontale, le rayon de visée va s'élever peu à peu par rapport
au sol. Il suffit alors de détecter à quelle distance le rayon passe
exactement à l'altitude souhaitée
égal à zéro lui aussi. On peut calculer la trajectoire du rayon de visée par
la méthode indiquée précédemment. Puisque l'observateur est au ras de la mer
et vise à l'horizontale, le rayon de visée va s'élever peu à peu par rapport
au sol. Il suffit alors de détecter à quelle distance le rayon passe
exactement à l'altitude souhaitée ![]() .
Alors, en vertu du principe de retour inverse de la lumière, cette distance est aussi
la distance apparente de l'horizon vu du point d'altitude
.
Alors, en vertu du principe de retour inverse de la lumière, cette distance est aussi
la distance apparente de l'horizon vu du point d'altitude ![]() .
Ensuite, reprenant le programme initial, en fixant pour le point d'observation
l'altitude cible
.
Ensuite, reprenant le programme initial, en fixant pour le point d'observation
l'altitude cible ![]() et pour le point cible
la distance obtenue précédemment et l'altitude
et pour le point cible
la distance obtenue précédemment et l'altitude ![]() , on peut calculer le site apparent
de l'horizon optique, vu du point d'observation à l'altitude
, on peut calculer le site apparent
de l'horizon optique, vu du point d'observation à l'altitude ![]() .
.
Si l'observateur est très près du niveau de la mer (quelques centimètres
par exemple) l'horizon est situé dans une direction de visée pratiquement horizontale
et extrêmement proche de lui. Dans ce cas, les rayons lumineux considérés sont tellement
courts que la réfraction joue un rôle pratiquement négligeable.
En revanche, pour des altitudes supérieures à 1000m, la différence
avec la distance et le site que l'on trouverait de manière purement géométrique
(c.à.d. sans tenir compte de la réfraction) commence à être assez significative.
Ainsi, pour le Pic de Saint-Barthélemy, l'horizon géométrique est à
173 km avec un site de ![]() degrés, tandis que l'horizon optique se trouve
repoussé à 190.3 km, avec un site
degrés, tandis que l'horizon optique se trouve
repoussé à 190.3 km, avec un site
![]() degrés. La distance angulaire
de l'horizon optique est alors
degrés. La distance angulaire
de l'horizon optique est alors
![]() degrés. On voit que l'horizon
marin vu du sommet du Pic de Saint-Barthélemy est rehaussé de
degrés. On voit que l'horizon
marin vu du sommet du Pic de Saint-Barthélemy est rehaussé de ![]() degrés environ
à cause de la réfraction atmosphérique.
degrés environ
à cause de la réfraction atmosphérique.
Si dans la méthode de détermination de l'horizon que nous venons
juste d'aborder, on fixe une altitude ![]() supérieure à 20 km environ
pour la cible, on s'aperçoit que lorsqu'il a atteint une certaine altitude,
le rayon lumineux, devient pratiquement rectiligne, c'est à dire que le
vecteur
supérieure à 20 km environ
pour la cible, on s'aperçoit que lorsqu'il a atteint une certaine altitude,
le rayon lumineux, devient pratiquement rectiligne, c'est à dire que le
vecteur ![]() devient pratiquement constant.
Ceci est dû au fait qu'à partir d'une certaine altitude, il n'y a plus assez d'air
pour dévier les rayons, et c'est alors la loi de propagation (rectiligne) dans le
vide qui s'applique.
devient pratiquement constant.
Ceci est dû au fait qu'à partir d'une certaine altitude, il n'y a plus assez d'air
pour dévier les rayons, et c'est alors la loi de propagation (rectiligne) dans le
vide qui s'applique.
En calculant l'angle que fait le vecteur ![]() , lorsqu'il devient
constant, avec l'axe
, lorsqu'il devient
constant, avec l'axe ![]() (qui est, rappelons-le, la direction de visée dans le problème
précédent), on en déduit le haussement apparent d'un objet extra-atmosphérique
situé exactement à l'horizon pour l'observateur. C'est donc aussi l'angle de
haussement du soleil lorsqu'il se couche ou se lève en mer ou en plaine.
(qui est, rappelons-le, la direction de visée dans le problème
précédent), on en déduit le haussement apparent d'un objet extra-atmosphérique
situé exactement à l'horizon pour l'observateur. C'est donc aussi l'angle de
haussement du soleil lorsqu'il se couche ou se lève en mer ou en plaine.
La Figure 2 illustre la situation examinée: l'observateur se trouve au point ![]() (en plaine ou au ras de la mer), et observe l'horizon, donc à l'horizontale, dans la direction
(en plaine ou au ras de la mer), et observe l'horizon, donc à l'horizontale, dans la direction ![]() .
Toutefois, à cause de la réfraction atmosphérique, le rayons lumineux qu'il voit n'est
pas la droite
.
Toutefois, à cause de la réfraction atmosphérique, le rayons lumineux qu'il voit n'est
pas la droite ![]() , mais la courbe en pointillé qui passe par
, mais la courbe en pointillé qui passe par ![]() et
et ![]() .
A partir d'une certaine altitude, cette courbe devient droite comme on le voit
sur la figure: à partir du point
.
A partir d'une certaine altitude, cette courbe devient droite comme on le voit
sur la figure: à partir du point ![]() , le rayon suit la direction de la droite
, le rayon suit la direction de la droite ![]() .
L'angle (noté
.
L'angle (noté ![]() sur la figure) de la déviation du rayon entre
sa direction initiale
sur la figure) de la déviation du rayon entre
sa direction initiale ![]() et sa direction finale
et sa direction finale ![]() , est le haussement
du soleil à son lever en plaine ou en mer.
, est le haussement
du soleil à son lever en plaine ou en mer.
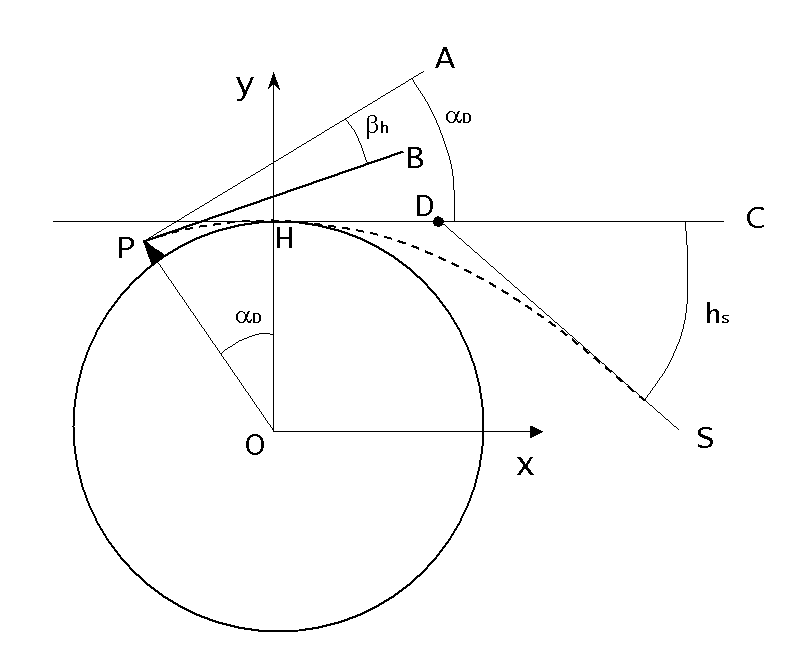
Figure 2: Différentes notations d'angles pour une observation
en mer (au point ![]() ) ou au sommet du Pic (au point
) ou au sommet du Pic (au point ![]() ).
).
Le calcul donne un haussement apparent de ![]() degrés. C'est à dire que
lorsque l'on observe le début du coucher de soleil, celui-ci est en fait déjà "couché"
du point de vue géométrique, puisque son diamètre apparent est d'environ
0.5 degrés. Ce résultat est un résultat classique de l'application de la
théorie de la réfraction atmosphérique.
degrés. C'est à dire que
lorsque l'on observe le début du coucher de soleil, celui-ci est en fait déjà "couché"
du point de vue géométrique, puisque son diamètre apparent est d'environ
0.5 degrés. Ce résultat est un résultat classique de l'application de la
théorie de la réfraction atmosphérique.
Pour trouver le haussement du soleil au moment de son lever
vu du sommet du Pic de Saint-Barthélemy, il suffit d'ajouter le haussement
du soleil au lever en plaine, ![]() , obtenu ci-dessus , et la déviation du rayon
lumineux entre le sommet du Pic et l'horizon optique vu du sommet du Pic.
, obtenu ci-dessus , et la déviation du rayon
lumineux entre le sommet du Pic et l'horizon optique vu du sommet du Pic.
La situation examinée est encore illustrée sur la Figure 2.
Cette fois, l'observateur est en haut du Pic, au point ![]() . Il regarde
dans la direction de l'horizon optique, c'est à dire dans la direction
. Il regarde
dans la direction de l'horizon optique, c'est à dire dans la direction ![]() sur la figure. Le rayon lumineux, en pointillé, passe alors par l'horizon
optique, qui est le point
sur la figure. Le rayon lumineux, en pointillé, passe alors par l'horizon
optique, qui est le point ![]() , puis continue son trajet vers le point
, puis continue son trajet vers le point ![]() ,
où il devient une droite. Le haussement du soleil à son lever au Pic est
donc l'angle entre la droite
,
où il devient une droite. Le haussement du soleil à son lever au Pic est
donc l'angle entre la droite ![]() et la droite
et la droite ![]() . Pour
connaître cet angle, il faut connaître l'angle entre
. Pour
connaître cet angle, il faut connaître l'angle entre ![]() et la droite
et la droite ![]() .
On voit sur la figure que cet angle entre
.
On voit sur la figure que cet angle entre ![]() et
et ![]() est égal à
est égal à
![]() ,
c'est à dire la distance angulaire terrestre entre le Pic et l'horizon optique
moins la valeur absolue du site de l'horizon optique vu du Pic
(notons que cette formule n'est valable que si
,
c'est à dire la distance angulaire terrestre entre le Pic et l'horizon optique
moins la valeur absolue du site de l'horizon optique vu du Pic
(notons que cette formule n'est valable que si ![]() est négatif, c'est à dire
si l'horizon est situé à une altitude inférieure au point de visée).
La droite
est négatif, c'est à dire
si l'horizon est situé à une altitude inférieure au point de visée).
La droite ![]() sur la figure est la droite horizontale passant
au point
sur la figure est la droite horizontale passant
au point ![]() . L'angle
. L'angle ![]() est un angle droit, tout comme l'angle
est un angle droit, tout comme l'angle
![]() , ce qui explique que l'angle
, ce qui explique que l'angle ![]() vaut bien
vaut bien ![]() .
.
Le haussement du soleil à son lever vu du Pic est donc égal à:
| (18) |
Le calcul donne un haussement apparent de ![]() degrés.
Le fait que l'observateur soit en altitude augmente encore le haussement
du soleil à son lever par rapport à une observation effectuée en plaine.
En conséquence, lorsque l'on voit le coucher de soleil vu du sommet du Pic, le
soleil est en fait "couché depuis un certain temps" (du point de vue géométrique).
degrés.
Le fait que l'observateur soit en altitude augmente encore le haussement
du soleil à son lever par rapport à une observation effectuée en plaine.
En conséquence, lorsque l'on voit le coucher de soleil vu du sommet du Pic, le
soleil est en fait "couché depuis un certain temps" (du point de vue géométrique).
Comme indiqué dans l'introduction, pour ce que nous voulons en faire ici, nous considérerons que les variations de l'indice de réfraction sont uniquement dues à la variation de la densité de l'air sec dans l'atmosphère, et nous supposerons en outre que cette densité est celle de "l'atmosphère standard", c'est à dire une atmosphère homogène horizontalement, et présentant un profil vertical proche de celui celui qui est observé en moyenne sur notre planète. Il faut donc définir précisément le profil standard utilisé, puis en déduire la formule de variation de l'indice de réfraction en fonction du lieu.
Dans le vide, l'indice de réfraction vaut 1 par définition.
Dans l'air, la vitesse est ralentie et l'indice ![]() est donc supérieur à 1.
Des mesures précises on montré que pour une pression
est donc supérieur à 1.
Des mesures précises on montré que pour une pression ![]() de 101325. Pa,
et une température
de 101325. Pa,
et une température ![]() de 273.16 K, l'indice de réfraction de l'air sec
de 273.16 K, l'indice de réfraction de l'air sec
![]() est donné par:
est donné par:
| (19) |
où ![]() est l'inverse de la longueur d'onde exprimée en
est l'inverse de la longueur d'onde exprimée en ![]() m,
c'est à dire:
m,
c'est à dire:
| (20) |
Pour le problème qui nous intéresse, on prendra une longueur
d'onde ![]() de 0.5
de 0.5 ![]() m, soit
m, soit ![]() . Pour les conditions
. Pour les conditions
![]() , l'indice de réfraction est alors:
, l'indice de réfraction est alors:
| (21) |
Ensuite, la propagation de la lumière dans l'air est telle que
le ralentissement de la lumière par rapport à la propagation dans le vide
est proportionnel à la densité de l'air traversé. Si on note ![]() la densité
de l'air et
la densité
de l'air et ![]() sa densité pour les conditions
sa densité pour les conditions
![]() , on a:
, on a:
Enfin, comme l'air est considéré ici comme un gaz parfait, on a:
| (23) |
où ![]() est la constante des gaz parfaits pour l'air sec (
est la constante des gaz parfaits pour l'air sec (![]() 287. J/K).
On en déduit donc finalement:
287. J/K).
On en déduit donc finalement:
| (24) |
Il est important de souligner que nous souhaitons non seulement calculer la déformation du paysage, mais aussi la trajectoire de rayons issus du soleil et parvenant au sol, afin de calculer leur déviation apparente. Cela nécessite donc de connaître l'indice de réfraction pour des couches atmosphériques situées non seulement près du sol, mais aussi très haut au dessus du sol (typiquement jusqu'à un cinquantaine de kilomètres). Pour cela, nous sommes alors obligés de connaître l'indice de réfraction et donc la densité de l'air jusqu'à ces altitudes élevées.
Nous notons ![]() l'altitude au-dessus du niveau de la mer.
l'altitude au-dessus du niveau de la mer.
Nous définirons notre atmosphère standard par une atmosphère d'air sec
(considéré comme un gaz parfait) en équilibre hydrostatique et composée de deux
couches superposées et de caractéristiques thermiques différentes,
dont l'interface (appelée tropopause) est située à l'altitude ![]() .
On a alors
.
On a alors
Les subtilités liées aux couches supérieures de l'atmosphère
(mésosphère, où la température se met à croître avec l'altitude, puis ionosphère,
où l'atmosphère devient ionisée et où l'indice
de réfraction se met à dépendre surtout de la densité d'électrons) sont ignorées,
car elles affectent peu les phénomènes que nous étudions. On considère donc qu'à
partir de l'altitude ![]() , l'atmosphère est isotherme jusqu'à l'infini. Notons
, l'atmosphère est isotherme jusqu'à l'infini. Notons
![]() la température au niveau
la température au niveau ![]() , et
, et ![]() la pression au niveau
la pression au niveau ![]() .
.
Remarque: Si l'on n'est pas intéressé par les calculs de position apparente du soleil, et que l'on s'intéresse seulement aux calculs de déformation du paysage, alors on peut ignorer la couche isotherme (stratosphère) dans les calculs. En effet, les reliefs terrestres sont trop peu élevés pour pénétrer jusqu'à la stratosphère, et donc les rayons lumineux d'un point à un autre du paysage sont toujours confinés dans la troposphère.
Nous appellerons ![]() la pression au niveau de la mer et
la pression au niveau de la mer et ![]() la température
au niveau de la mer. La valeur de ces deux quantités n'est pas spécifiée pour l'instant
afin de pouvoir les choisir proches des conditions observées.
la température
au niveau de la mer. La valeur de ces deux quantités n'est pas spécifiée pour l'instant
afin de pouvoir les choisir proches des conditions observées.
Notre atmosphère standard est donc définie par le profil thermique ![]() suivant:
suivant:
| (25) |
Il faut maintenant calculer le profil barique de l'atmopshère. Pour cela, nous utilisons le fait que nous avons supposé l'atmopshère en équilibre hydrostatique (par exemple au repos). On a alors:
où ![]() est l'accélération de la gravité
est l'accélération de la gravité ![]() m/s/s.
m/s/s.
Dans la troposphère, (26) donne:
| (27) |
et donc, puisque ![]() est non nul:
est non nul:
Dans la stratosphère isotherme, (26) donne:
| (29) |
et donc:
| (30) |
où
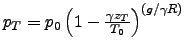 est
déterminé en substituant
est
déterminé en substituant ![]() dans (28), car le profil
de pression doit être continu en
dans (28), car le profil
de pression doit être continu en ![]() .
Le profil de pression est donc donné par:
.
Le profil de pression est donc donné par:
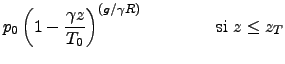 |
|||
![$\displaystyle p_T \; \exp \left[- \frac{g }{R T_T} (z-z_T)\right]\;\;\;\;\;\;\;\;\; {\rm si \;} z > z_T$](img172.png) |
(31) |
Finalement, le profil de densité s'exprime alors par:
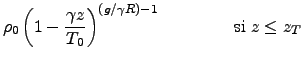 |
|||
![$\displaystyle \rho_T \; \exp \left[- \frac{g }{R T_T}(z-z_T) \right]\;\;\;\;\;\;\;\;\;\;\;\;\; {\rm si \;} z > z_T$](img175.png) |
(32) |
où
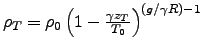 est la densité au niveau de la tropopause.
est la densité au niveau de la tropopause.
En utilisant la formule (22), on obtient le profil de l'indice de réfraction atmosphérique:
| (33) |
soit:
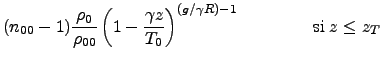 |
|||
![$\displaystyle (n_{00} -1) \frac{\rho_T}{\rho_{00}}\; \exp \left[- \frac{g }{R T_T}(z-z_T) \right]\;\;\;\;\;\;\;\;\;\;\;\;\; {\rm si \;} z > z_T$](img5.png) |
(34) |
Le gradient vertical de l'indice de réfraction s'écrit alors:
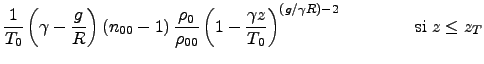 |
|||
![$\displaystyle \frac{- g}{R T_T}(n_{00} -1) \frac{\rho_T}{\rho_{00}}\; \exp \left[- \frac{g }{R T_T} (z-z_T)\right]\;\;\;\;\;\;\;\;\;\;\;\;\; {\rm si \;} z > z_T$](img27.png) |
(35) |
La méthode de calcul utilisée ici n'est pas la seule possible: il existe d'autres
méthodes pour évaluer la trajectoire de rayons lumineux dans des milieux réfringents.
Il existe notamment une méthode légèrement plus simple que celle décrite ci-dessus, et qui consiste
à considérer l'atmosphère comme une série de ![]() couches superposées, à l'intérieur
desquelles l'indice est uniforme. Nous appellerons cette méthode "méthode des dioptres
superposés", car à l'interface de chaque couche d'indice uniforme, il existe une discontinuité
de la valeur de l'indice, ce qui crée donc un dioptre. Dans cette méthode, l'atmosphère est
donc considérée comme une superposition de
couches superposées, à l'intérieur
desquelles l'indice est uniforme. Nous appellerons cette méthode "méthode des dioptres
superposés", car à l'interface de chaque couche d'indice uniforme, il existe une discontinuité
de la valeur de l'indice, ce qui crée donc un dioptre. Dans cette méthode, l'atmosphère est
donc considérée comme une superposition de ![]() dioptres d'indice uniforme..
dioptres d'indice uniforme..
La méthode de calcul que nous avons décrit illustrée ici est beaucoup plus précise et plus universelle que celle des dioptres superposés, car elle peut s'appliquer telle quelle dès que l'expression exacte de l'indice de réfraction est connue. Cette méthode est notamment valable quelle que soit la distance entre l'observateur et la cible observée et quelle que soit la direction du rayon calculé.
La méthode des dioptres superposés est moins universelle en ce sens par exemple qu'elle ne permet pas de décrire correctement la trajectoire d'un rayon lumineux qui demeure dans une même couche tout au long de son parcours. Par construction, avec cette méthode, la trajectoire d'un tel rayon sera un segment de droite, alors que dans la réalité, du fait des variations spatiales continues de l'indice de réfraction, la trajectoire du rayon est incurvée. Cette méthode des dioptres superposés est donc plutôt mieux adaptée au calcul des rayons inclinés que pour le calcul des rayons proches de l'horizontale.
Or, dans la réalité, les rayons qui ont la plus forte courbure locale sont ceux qui sont les plus proches de l'horizontale. Ceci est démontré sur le lien suivant:
courbure locale d'un rayon lumineux dans un milieu à réfringence continument variable
La méthode des dioptres superposés ne permet pas de rendre compte de cette
réalité.
On peut dire que dans la méthode des dioptres superposés, la discrétisation, étant adoptée a priori et selon la verticale, n'est pas pertinente pour des rayons qui ont des trajets horizontaux, car ces rayons sont alors très mal échantillonnés. Par exemple si on adopte des couches de 100m d'épaisseur, des rayons horizontaux proches de la surface terrestre peuvent voyager, avec ce modèle, sur une distance de plus de 140 km sans être aucunement échantillonnés: l'échantillonage est alors très médiocre pour ces rayons, à l'endroit même où il devrait être le meilleur possible, du fait de la courbure locale maximale de ces rayons dans la réalité, comme on vient de le voir.
La méthode décrite dans la note ci-dessus assure en revanche un échantillonage uniforme des rayons sur toute leur longueur, ce qui conduit à une méthode de discrétisation de problème bien mieux posée et bien plus pertinente.
Ajoutons que d'un point de vue conceptuel, cette méthode des dioptres superposés pourrait laisser croire que les rayons qui se propagent dans une direction proche de l'horizontale sont moins courbés que ceux qui ont une inclinaison notable, alors que c'est précisément l'inverse qui est vrai. En fait, cette méthode étant imprécise par nature, c'est son imprécision qui produit ce résultat. Alors, si on se contente d'examiner les résultats produits par cette méthode et qu'on les adopte comme vérité, on en tirera la conclusion que les rayons horizontaux sont moins courbés que leurs homologues inclinés, ce qui est faux en réalité.
En revanche, pour des trajets de rayons dans l'atmosphère suffisament longs et inclinés
par rapport à l'horizontale, cette méthode des dioptres superposés, bien qu'imprécise, donne des résultats
relativement satisfaisants en première approximation, car alors la discrétisation est pertinente
sur une partie importante du trajet, du fait de l'inclinaison des rayons.
Pour de tels rayons,
la majeure partie du trajet s'effectue de façon inclinée et donc le modèle des dioptres superposés
n'est pas trop imprécis, pourvu que le nombre de couches ![]() soit choisi de façon adéquate
par rapport au problème.
soit choisi de façon adéquate
par rapport au problème.
Reste qu'avec le développement des moyens automatiques de calculs, il n'y a plus de raison de continuer à utiliser la méthode des dioptres superposés, potentiellement mal échantillonée et imprécise, comme on vient de le voir. Cette méthode était bien adaptée pour des calculs "à la main" ou avec les très faibles moyens de calculs dont on disposait avant l'ère de l'électronique, du fait du nombre très modique d'opérations qu'elle requiert, mais elle nécessitait de grandes précautions dans son application. De nos jours, des méthodes légèrement plus couteuses en nombre d'opérations mais plus universelles et plus précises devraient être logiquement privilégiées.